Optimal system of loops
on an orientable surface
Éric
Colin de Verdière and Francis
Lazarus.
Appeared in Discrete
& Computational Geometry. 33(3): 507 - 534, March 2005.
(also presented at 43rd IEEE Symposium on Foundations of Computer Science (FOCS
2002))
Download journal version (final except before copy editing)[gzipped postscript (509 Ko)]
[pdf
(593 Ko)]
Download conference version (© 2002 IEEE) [postscript (300 Ko)]
[pdf (226 Ko)]
Abstract
Every compact orientable boundaryless surface M can
be cut along simple loops with a common point $v_0$, pairwise
disjoint except at v0, so that the resulting surface is a
topological disk; such a set of loops is called a system of
loops for M. The resulting disk may be viewed as a polygon
in which the sides are pairwise identified on the surface; it is
called a polygonal schema. Assuming that M is a
combinatorial surface, and that each edge has a given length, we are
interested in a shortest (or optimal) system of loops
homotopic to a given one, drawn on the vertex-edge graph of M.
We prove that each loop of such an optimal system is a shortest loop
among all simple loops in its homotopy class. We give an algorithm
to build such a system, which has polynomial running time if the
lengths of the edges are uniform. As a byproduct, we get an
algorithm with the same running time to compute a shortest simple
loop homotopic to a given simple loop.
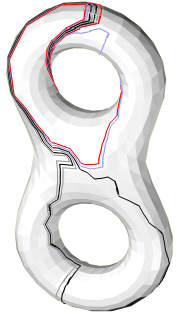
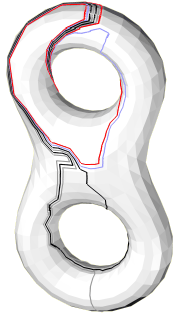
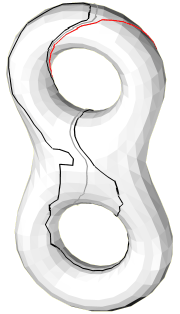
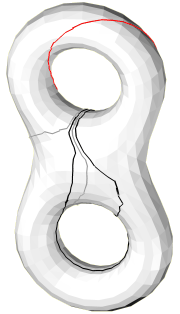
Implementation
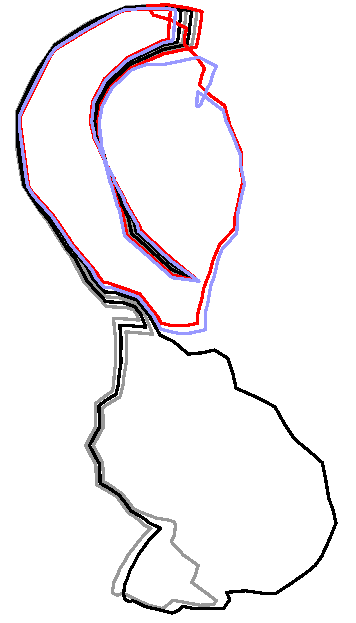
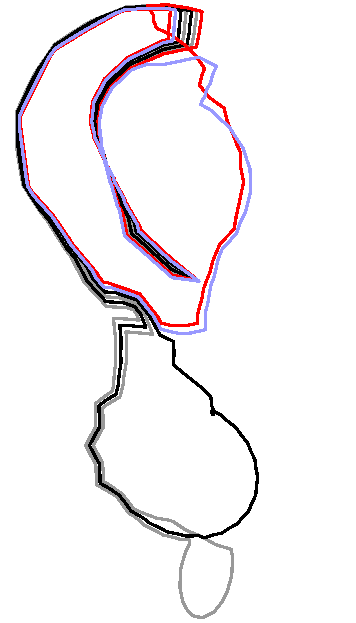
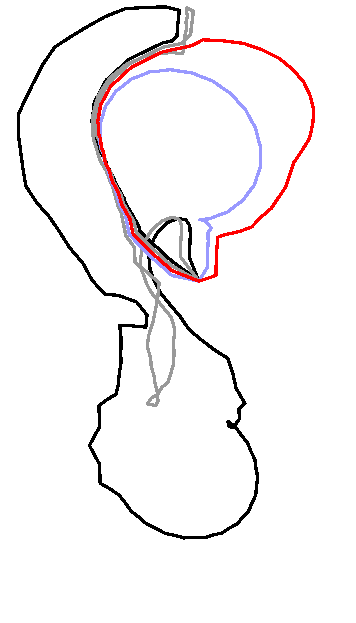
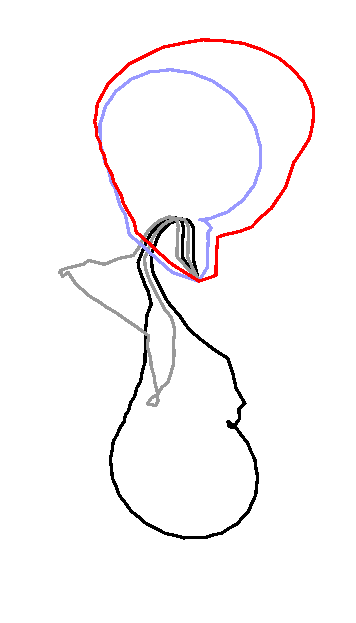
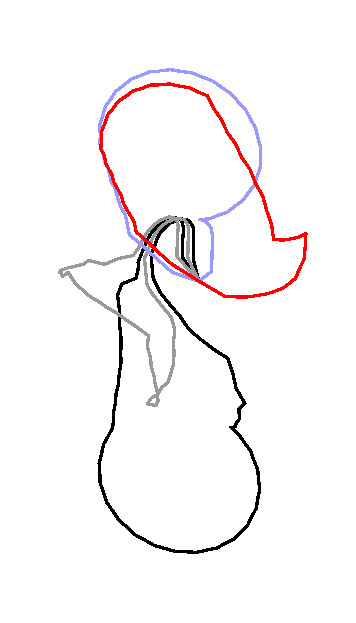
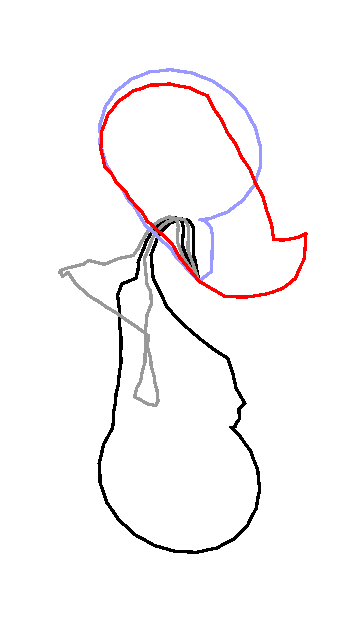
The optimization algorithm is based on an elementary step which replaces
each loop in turn by a shorter homotopic loop. The journal and
conference versions of the paper slightly differs in the implementation of
this elementary step. Specifically, the implementation in the journal
version avoids the computation of the (partial) universal covering of a certain
cylinder as described in the conference version. The figures below
refer to the journal version of the elementary step.
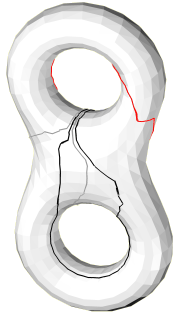
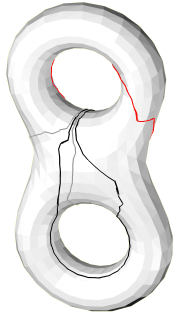
The loops
are spread apart the edges they should follow in order to distinguish
several loops when they walk along a same edge.