|
Francis Lazarus Researcher at CNRS |
|
|
|
|
| |||
|
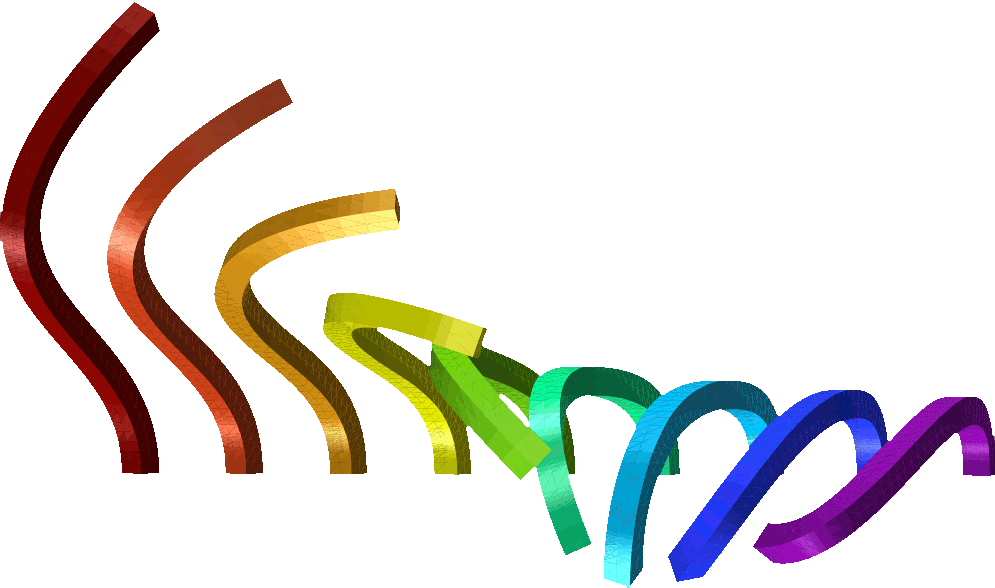
Francis Lazarus Researcher at CNRS |
|
|
|
|
| |||
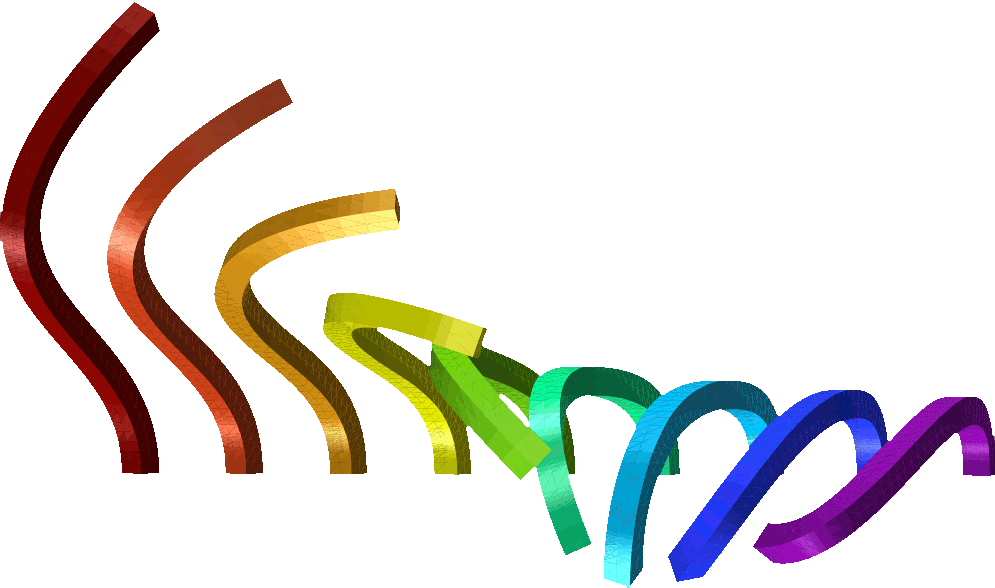
Francis Lazarus
Laboratoire G-SCOP, UMR CNRS 5272
46, avenue Félix Viallet
38031 Grenoble Cedex 1
FRANCE
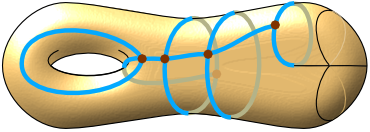
The Hevea project.
Some old pictures and animations
Selected publications:
Hyperbolic Plane in E³. Vincent Borrelli, Roland Denis, Francis Lazarus, Mélanie Theillière and Boris Thibert. 2023, arXiv version.
A Linear Bound for the Colin de Verdière Parameter μ for Graphs Embedded on Surfaces. Camille Lanuel, Francis Lazarus and Rudi Pendavingh. 39th European Workshop on Computational Geometry (EuroCG'23). arXiv version.
Algorithms for Length Spectra of Combinatorial Tori. Vincent Delecroix, Matthijs Ebbens, Francis Lazarus, and Ivan Yakovlev. Proc. SoCG'23. arXiv version.
A Universal Triangulation for Flat Tori. Francis Lazarus and Florent Tallerie. Proc. SoCG'22, 2022. Version arXiv. Some nice pictures on IMAGINARY.org.
Algorithms for Contractibility of Compressed Curves on 3-Manifold Boundaries. Erin Wolf Chambers, Francis Lazarus, Arnaud de Mesmay, and Salman Parsa. Proc. SoCG'21, 2021. ![[PDF]](GIFs/pdf.gif){kind=small}
arXiv version.
Computing the Geometric Intersection Number of Curves.
Vincent Despré and Francis Lazarus. Journal of the ACM, 66(6):1-49, 2019. (Also appeared with
Best paper award in Proc. SoCG'17 ).
An explicit isometric reduction of the unit sphere into an arbitrarily small ball.
E. Bartzos, V. Borrelli, R. Denis, F. Lazarus, D. Rohmer and B. Thibert,
Foundations of Computational Mathematics (FoCM), pp. 1-28, 2017. doi:10.1007/s10208-017-9360-1.
Some Triangulated Surfaces without Balanced Splitting. Vincent Despré and Francis Lazarus. Graphs and Combinatorics, 32(6): 2339-2353, 2016. doi:10.1007/s00373-016-1735-6. arXiv version.
Finding shortest non-trivial cycles in directed graphs on surfaces.
Sergio Cabello,
Éric Colin de Verdière and
Francis Lazarus. Journal of Computational Geometry,
7(1):123-148, 2016. (Also appeared in Proc. SoCG'10)
Combinatorial Graphs and Surfaces from the
Computational and Topological Viewpoint
Followed by some notes on
The Isometric Embedding of the square Flat
Torus. Habilitation thesis defended on September 16, 2014 .
Isometric embeddings of the square flat torus in ambient space. Vincent Borrelli, Saïd Jabrane, Francis Lazarus and Boris Thibert. Ensaios
Matemáticos, 24:1-91, 2013 .
The Nash-Kuiper process for curves. Vincent Borrelli, Saïd Jabrane, Francis Lazarus and Boris Thibert. Actes du séminaire de théorie spectrale et géométrie, 30:1-19, 2011-2012. .
On the homotopy test on surfaces with boundaries. Julien Rivaud and
Francis Lazarus. 28th European Workshop on Computational Geometry (EUROCG), pp. 189-192, 2012. .
On the homotopy test on surfaces. Francis Lazarus and
Julien Rivaud. proc. IEEE Symposium on Foundations of Computer Science
(FOCS)proc. IEEE Symposium on Foundations of Computer Science
(FOCS), pp. 440-449, 2012. Submitted version . A more detailed arXiv version.
Flat tori in three dimensional space and convex integration.
Vincent
Borrelli,
Saïd Jabrane,
Francis Lazarus
and Boris
Thibert.
Proceedings of the National Academy of Sciences of the United
States of America (PNAS), 109(19):7218-7223,
2012. A (long) abstract. Submitted version and a
nice picture.
Finding cycles with topological properties in embedded graphs.
Sergio Cabello,
É. Colin de Verdière,
Francis Lazarus. SIAM Journal on Discrete Mathematics, 25:1600-1614, 2011.
Algorithms for the edge-width of an embedded graph.
Sergio Cabello,
É. Colin de Verdière,
Francis Lazarus. Computational Geometry: Theory and
Applications, 45(5-6):215-224, 2012. (Also appeared in Proc. SoCG'10)
Persistence-sensitive simplification of functions on surfaces
in linear time. Dominique Attali, Marc Glisse, Samuel Hornus,
Francis Lazarus and Dmitriy Morozov.TOPOINVIS'09
(Topological
Methods In Data Analysis and Visualization), 23-24
Feb. 2009, Snowbird.
Additional pictures.
Homotopic Fréchet distance between curves --- or, walking your dog in the woods in polynomial time.
E. W. Chambers,
É. Colin de Verdière,
J. Erickson,
Sylvain Lazard,
Francis Lazarus,
Shripad Thite.
Computational Geometry: Theory and Applications, 43:295-311,
2010.
(Also appeared in
Proc.
SoCG'08 .)
Splitting (complicated) surfaces is hard.
E. W. Chambers,
É. Colin de Verdière,
J. Erickson,
F. Lazarus, and
K. Whittlesey.
Computational Geometry: Theory and Applications, 41:94-110, 2008 (Also appeared in Proc. SoCG'06). Submitted version
Optimal Pants Decompositions and Shortest Homotopic Cycles on an Orientable Surface. É.
Colin de Verdière and F. Lazarus. Journal of the ACM, 54(4),
art. 18, jul. 2007. (Also appeared in Proc. Graph Drawing, 2003). Submitted version
Optimal System of Loops on an Orientable Surface. É. Colin de Verdière and F. Lazarus. Discrete & Computational Geometry. 33(3): 507 - 534, 2005. (Also appeared in Proc. FOCS'02.) Abstract and electronic copies.
Computing a Canonical Polygonal Schema of an Orientable Triangulated
Surface. F. Lazarus, M. Pocchiola,
G.
Vegter and A. Verroust.
17th
ACM Symposium on Computational Geometry, pp. 80-89, June 2001. Submitted version
Cutting and Stitching: Converting Sets of Polygons to Manifold Surfaces. A. Guéziec, G. Taubin, F. Lazarus and W. Horn. IEEE Transactions on Visualization and Computer Graphics, 7(2):136-151, 2001.
Extracting skeletal curves from 3D scattered data. A. Verroust and F. Lazarus. The Visual Computer. Springer, 16(1):15-25, 2000.
Level Set Diagrams of Polyhedral Objects. F. Lazarus and A. Verroust. ACM Solid Modeling'99. June 1999, Ann-Arbor, Michigan, USA.
A Framework for Streaming Geometry in VRML. A. Guéziec, G. Taubin, F. Lazarus and W. Horn. IEEE Computer Graphics and Applications, 19(2):68-78, 1999.
Three-dimensional metamorphosis: a survey. F. Lazarus and A. Verroust. The Visual Computer, 14(8-9):373-389, 1998.
Progressive Forest Split Compression. G. Taubin, A. Guéziec, W. Horn and F. Lazarus. Siggraph'98 Conference Proceedings. August 1998, Orlando, Florida, USA.
Geometry coding and VRML. G. Taubin, W. Horn, F. Lazarus and J. Rossignac. Proceedings of the IEEE, 86(6):1228-1243, 1998.